Understanding the Parabola: Definition and Coefficient Effects

A quadratic equation has the form:

y = ax² + bx + c (e.g. 3x²+4x+50)

a, b , c, could be any real values and can be either positive or negative

a ,b, c are called the coefficients of the quadratic equation, and they affect the shape of the quadratic equation parabola in the following manner:

Coefficient a: Direction and Width

- Sign of a:
- a > 0 → Parabola opens upward

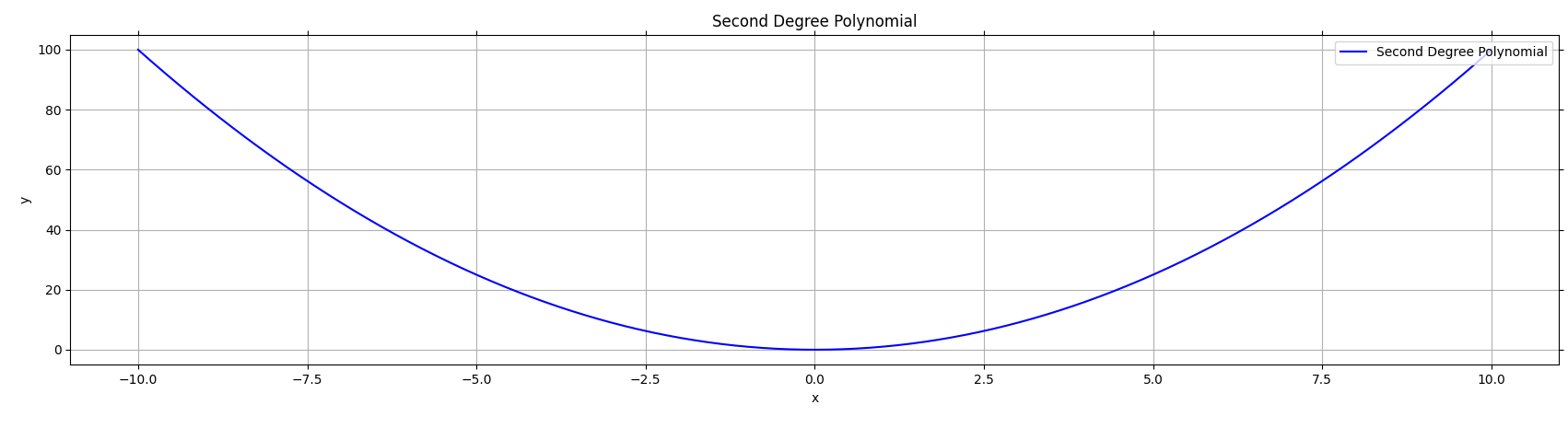
Figure 1 : when a is positive (a>0), parabola is upward

- a < 0 → Parabola opens downward

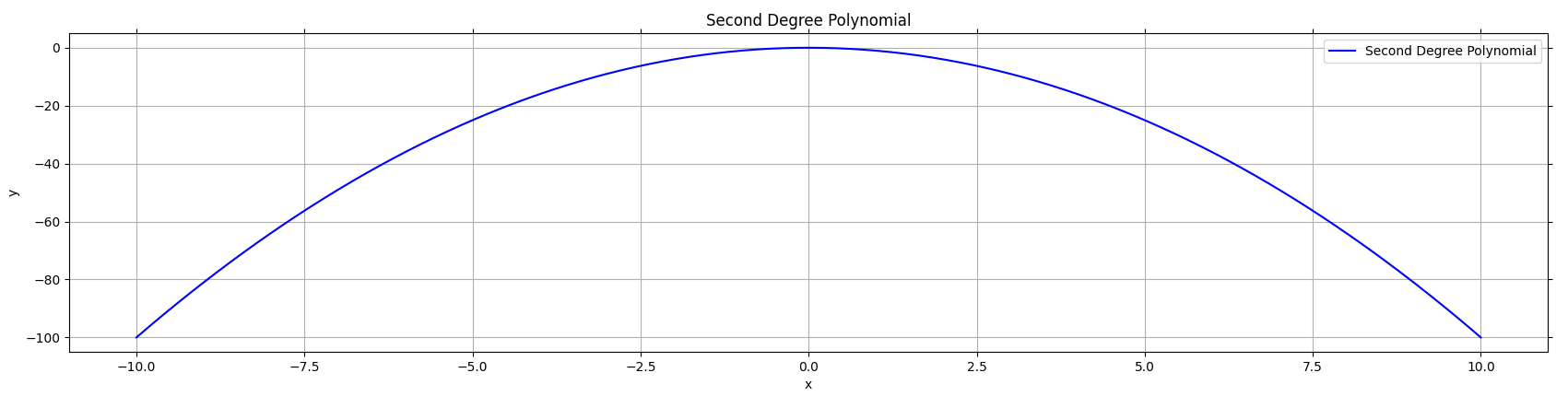
Figure 2 Negative a, downward curve

- Magnitude of a:
- Larger |a| → Narrower parabola
- Smaller |a| → Wider parabola

Example:
If a = 10 and a = 2, both open upward, but a = 10 gives a narrower parabola than a = 2.

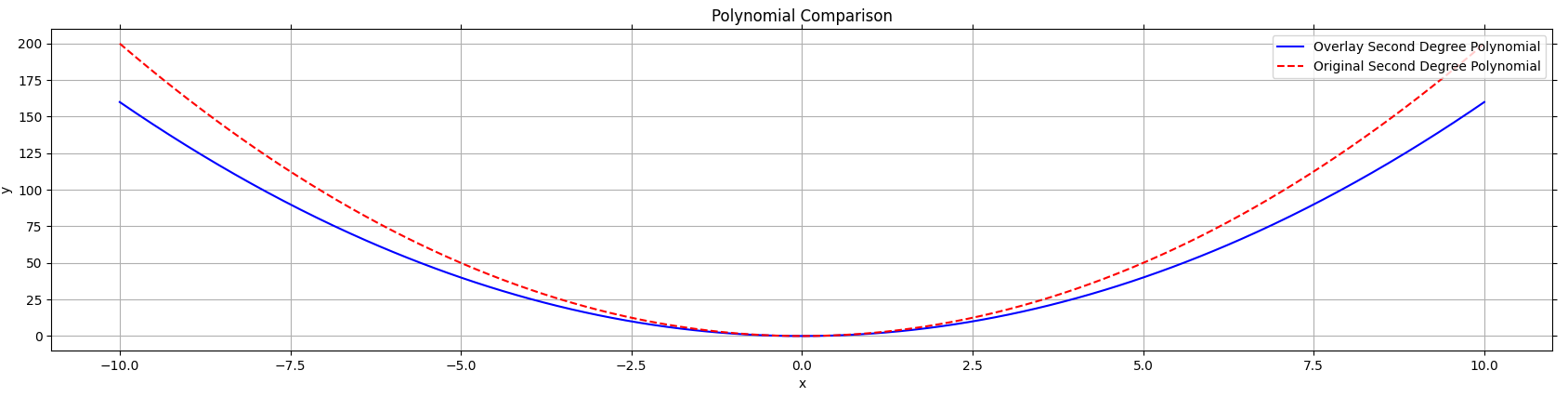
Figure 3: For two parabolas, if a1>a2, then parabola one is narrower than the second

In the figure above, notice how the first (red) parabola (a=10) is narrower than the first (blue) parabola (a=2).

Coefficient b: Tilt and Vertex Shift

- Controls the horizontal shift and tilt of the parabola
- Affects the symmetry and vertex location using:

x₀ = –b / 2a

- If b is large compared to a, the curve appears tilted, and the vertex shifts significantly.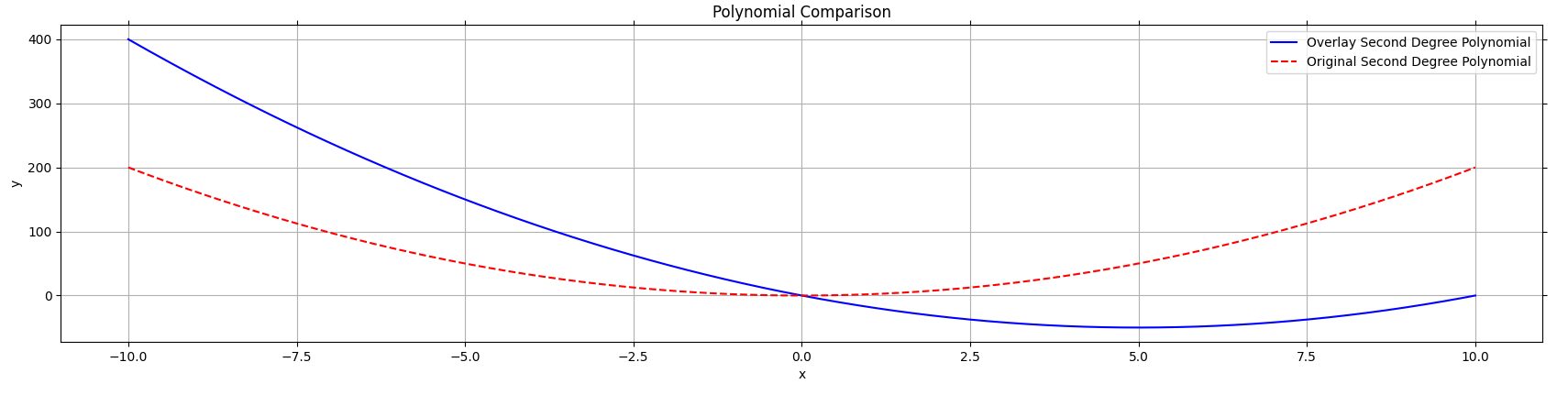

Figure 4: the coefficient b in the parabola determines the tilt (how symmetric it is around the center)

The figure above shows that the blue curve is tilted relative to the red curve
Note: If b >> a, the parabola is so tilted to the point of become a simple line (think about the equation of the parabola and why this happens).

Coefficient c: Y-Intercept

- Determines where the parabola cuts the Y-axis
- c > 0 → Intercepts above the X-axis
- c < 0 → Intercepts below the X-axis

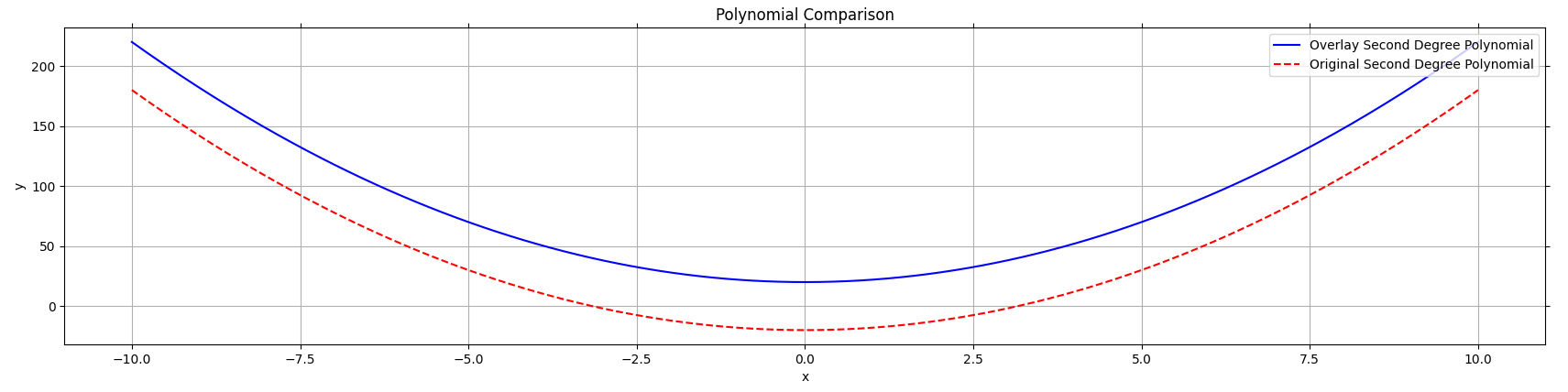
Figure 5: The red graph has a negative c value while the blue has a positive c value

Roots: X-Axis Intersections

- Roots are the x-values where y = 0
- If the roots are real, the parabola intersects the X-axis at the root values

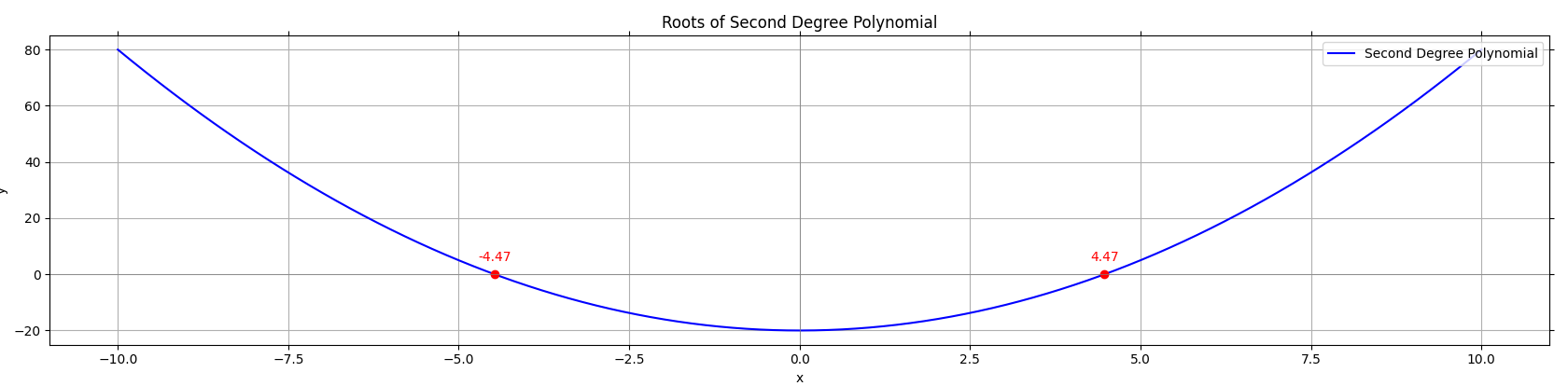
Figure 6: This parabola has real roots, thus intersects x axis at -4.47 and 4.47. These are called roots of a polynomial.

- If the roots are imaginary, the parabola does not touch the X-axis

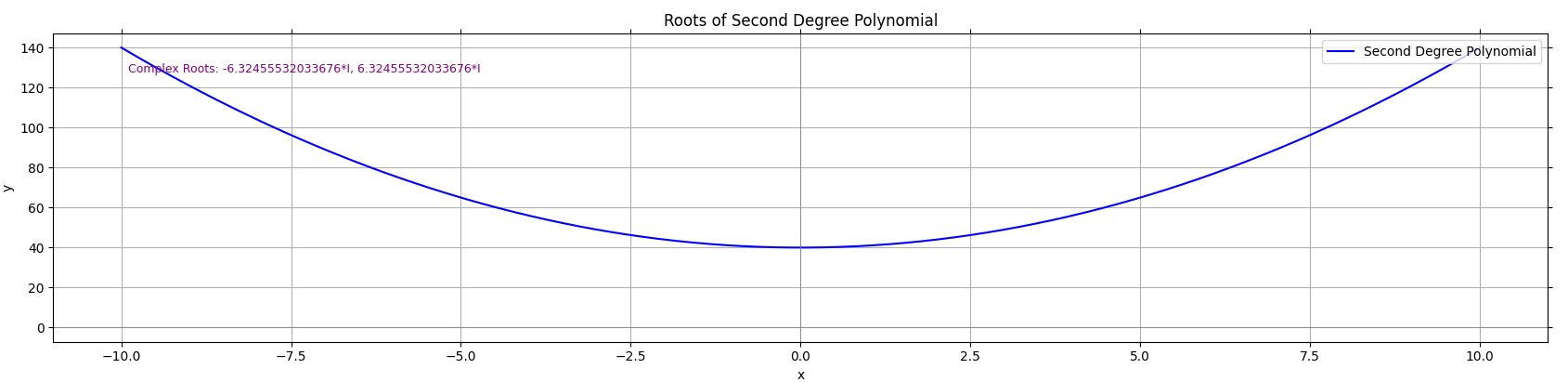
Figure 7: This parabola does not intersect or touch the x-axis, thus its roots are not real (imaginary roots)

Example:

Sample Table: Effect of Coefficients on Parabola

a	b	c	Parabola Description
2	0	-4	Opens upward, cuts Y below X-axis
-3	6	1	Opens downward, vertex shifted right
1	10	45	Wide upward parabola, tilted left
-5	-2	-8	Narrow downward parabola, Y-intercept below 0